Es un trabajo con fuerte hincapié en el uso de un software específico llamado Geogebra (se puede descargar en http://www.geogebra.at/download); a través de su uso, se pretende establecer relaciones de conceptos que impliquen:
La idea de este trabajo surge por dos razones principalmente:
Casi siempre se asocia a Sistemas de Ecuaciones las de tipo lineal, sin tener en cuenta que poseemos una riqueza muy grande para trabajar cuando comenzamos a combinar diferentes tipos de gráficas; en este caso sólo abarcamos rectas y cónicas, dejando lugar para ampliar a otras, de tipo logarítmica, exponencial, etc. La versatilidad del programa permite reconocer la ecuación que representa cada cónica, sus invariantes. También otorga la posibilidad de que al interior de cada cónica se puedan analizar las componentes que definen las variaciones internas de las mismas. A su vez, la posibilidad de que el programa me diga en qué lugar están los puntos de intersección me brinda herramientas para conocer el/los par/es ordenado/s que es/son solución del sistema referido.
Por todo lo anterior, más la facilidad de uso del programa y su interfaz muy amigable, este trabajo que en primera instancia parece engorroso se torna ameno, bastante didáctico, y además puede ser realizado en un tiempo bastante reducido.
Una variable didáctica que se tuvo en cuenta es trabajar con cónicas que tienen ejes paralelos a los ejes cartesianos y en lo posible centrados en el origen.
Otra variable es que el programa da a conocer la ecuación en su forma general de 2º Grado (A x2 + B y2 + C x + D y + E = 0), lo que obliga al alumno a completar cuadrados si desea escribir la ecuación en forma canónica.
Es un trabajo abierto, brinda la posibilidad de complejizar desde lo gráfico (por ej. trabajando con graficas no centradas en el origen); desde lo analítico (por ej. resolver los sistemas), así como también ampliar a través de la inclusión de gráficas de otras funciones, etcétera.
La importancia didáctica radica en:
Último año de Escuela Media.
Geometría, álgebra y análisis matemático.
1. Laboratorio de informática o PC personal.
2. Bibliografía utilizada:
a) Matemáticas para Bachillerato, de Miguel de Guzmán, editorial Anaya.
b) Geometría analítica del plano y del espacio, de Donato Di Pietro, editorial Alsina.
c) Matemática 4, de Nelly de Tapia, editorial Estrada.
Alumnos y docentes.
Estimo que podría pensarse en 4 h. cátedra por cada actividad prevista.
Creo que el trabajo es bastante interesante, porque implica desplegar una práctica distinta de las convencionales y da origen a la utilización de una variedad de estrategias, contemplando el uso y puesta en juego de conceptos básicos referidos a rectas, ecuaciones canónicas de cada una de las cónicas, así como también el conocimiento de propiedades o la investigación de las mismas para poder compatibilizar lo gráfico con lo analítico.
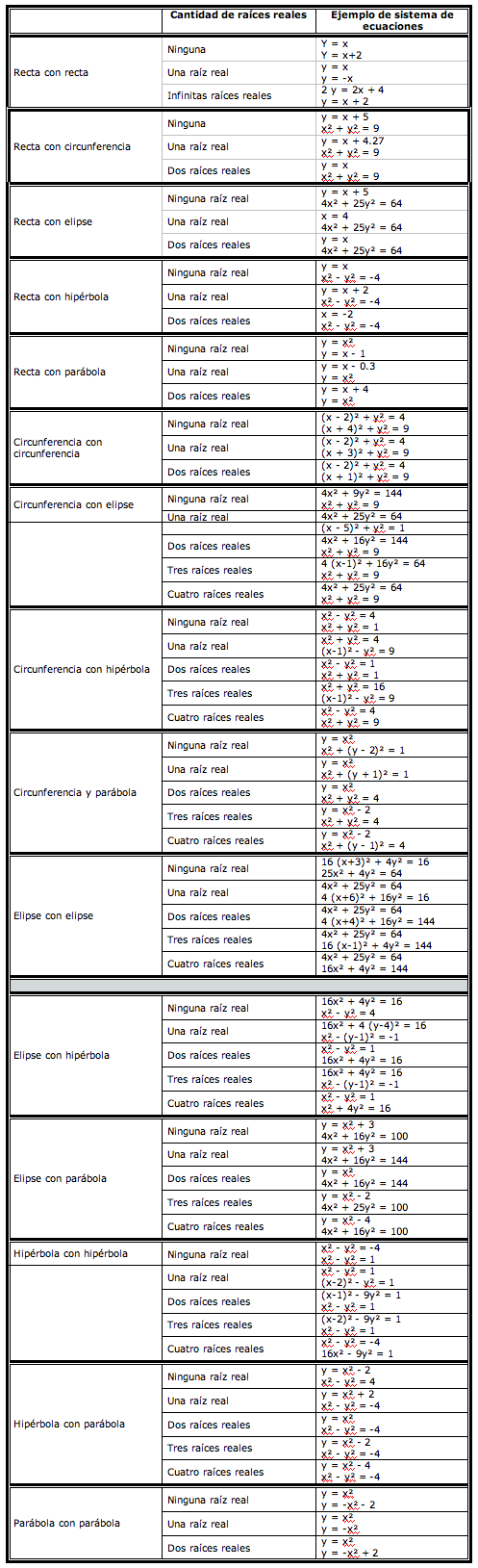
Un ejemplo de lo que se puede lograr como trabajo final sería:
a) Pensar en cuáles son las posibilidades de combinar entre rectas y cónicas:

b) Con la ayuda del graficador, poder ir logrando algunos sistemas de ejemplos; la idea es que puedan lograrse de la forma más sencilla posible, a fin de luego poder corroborar analíticamente lo logrado con la PC.