Descargar Aplicación

Programa para realizar construcciones equivalentes a las realizadas con regla y compás, y analizarlas dinámicamente.

Infomación

Debajo de la barra del menú se encuentra otra barra con botones para diferentes opciones del programa. Luego de cliquear sobre cada botón se muestran indicaciones muy útiles en una barra en la parte inferior de la pantalla. Si no se ve esta barra, maximizar la ventana del programa.

Las características de los botones son las siguientes:

Botón	Nombre	Ubicación en el menú / tecla abreviada	Función / modo de empleo
	Punto	Figuras -> Punto / P	Marca| un punto. Cliquear sobre el área de trabajo del programa. Las propiedades del punto, como el tipo y el color, se pueden definir cliqueando sobre el punto creado con el botón derecho del mouse.
	Recta	Figuras -> Recta / L	Marca dos puntos y traza una recta que pasa por ellos. Cliquear en dos lugares distintos.
	Segmento	Figuras -> Segmento / S	Traza un segmento. Marcar los dos puntos de los extremos.
	Semirrecta	Figuras -> Semirrecta / R	Traza una semirrecta. Marcar dos puntos. La semirrecta comienza en el primero y pasa por el segundo.
	Círculo	Figuras -> Circunferencia / C	Traza una circunferencia. Marcar dos puntos; el primero es el centro, la distancia entre ambos es el radio.
	Círculo (3)	Figuras -> Circunferencia (3) / 3	Traza una circunferencia. Marcar un punto. Éste es el centro de la circunferencia. Seleccionar otros dos, marcados previamente. La distancia entre ellos es el radio de la circunferencia.
	Intersección	Acciones -> Intersección / I	Marca el/los puntos de intersección de dos objetos (por ejemplo, una recta y una circunferencia). Seleccionar los dos objetos. No admite ángulos ni puntos.
	Punto sobre objeto	Figuras -> Punto sobre objeto / O	Marca un punto sobre un objeto (por ejemplo una recta o una circunferencia). Cliquear sobre el objeto en el lugar donde se desea marcar el punto.
	Mover punto	Acciones -> Mover / M	Mueve un punto. Cliquear sobre el punto (creado previamente) y arrastrarlo con el mouse.
	Mover sobre objeto	Acciones -> Mover sobre objeto / J	Mueve un punto sobre un objeto (por ejemplo, una recta o una circunferencia). Seleccionar el objeto y luego el punto (ambos creados previamente). El punto se asocia al objeto y se mueve con él, cambiando la forma de otras construcciones a las que éste pudiera estar asociado.
	Trayectoria de puntos	Acciones -> Trayectoria / T	Deja una traza fina al mover un punto. Es útil para graficar curvas o funciones definidas geométricamente, por ejemplo utilizando el archivo machine.car, que trae el programa. Seleccionar el punto, luego moverlo desplazando otro punto con "Mover punto" o "Mover sobre objeto".
	Punto medio	Figuras -> Punto medio / D	Marca el punto medio entre dos puntos. Marcar o seleccionar los dos puntos.
	Perpendicular	Figuras -> Recta perpendicular / V	Traza una recta perpendicular. Seleccionar una recta (o semirrecta o segmento, creados previamente), luego marcar o seleccionar un punto.
	Paralela	Figuras -> Recta paralela / 1	Traza una recta paralela. Seleccionar una recta (o semirrecta o segmento, creados previamente), luego marcar o seleccionar un punto exterior a ella.
	Ángulo	Figuras -> Ángulo / A	Traza un arco correspondiente al ángulo en sentido antihorario, definido por tres puntos. Marcar o seleccionar tres puntos; el segundo es el vértice.
	Editar propiedades	Acciones -> Editar / E	Abre una ventana con opciones de las propiedades del objeto que se seleccione. Permite definir el nombre de los objetos creados, el color, la forma de los puntos y el grosor de las líneas. Cuando se selecciona un ángulo se observa su medida en grados. Seleccionar las opciones mostradas en la ventana.
	Ocultar/ mostrar	Acciones -> Ocultar / H	Oculta los objetos seleccionados o vuelve a mostrar objetos ocultos. Cliquear sobre los objetos que se desean ocultar. Los objetos ocultos se muestran en color más tenue que los visibles o desaparecen. Esto depende del botón "Mostrar / ocultar todo".
	Expresión	Acciones -> Expresión / X	Introduce una expresión. Seleccionar el objeto, introducir las variables de la expresión en la ventana que aparece. Se puede incluir, por ejemplo, un número, o el nombre de algún objeto creado. En este caso muestra alguna de las características numéricas del objeto, como el radio de una circunferencia, y se actualiza al modificar el objeto.
	Color por defecto	Opciones -> Color por defecto / Ctrl+1, ...a Ctrl+6	Determina el color de los objetos que se crearán. Cliquear en la ventana el color elegido y luego generar el objeto. Las opciones son negro, azul, marrón, verde, rosa y cian. Es útil para diferenciar distintas figuras, etapas, o "jerarquías" en la construcción.
	Borrar trayectorias	Acciones -> Borrar trayectorias / F6	Borra la trayectoria de puntos, si se empleó esta opción previamente.
	Ocultar/ mostrar todo	Opciones -> Mostrar todo / F8	Muestra, en color más tenue, los elementos definidos como ocultos. Al cliquear por segunda vez, oculta los objetos mostrados.

Autora: M. Valeria Machiunas

Recomendación docente

Se espera que los alumnos elaboren conjeturas acerca de qué clase de cuadriláteros pueden obtenerse tomando como vértices los puntos medios de un cuadrilátero dado, y las prueben. Los siguientes problemas para resolver con el programa Regla y compás les permitirán a los alumnos indagar sobre un buen número de cuadriláteros, en relativamente poco tiempo, comparado con el trabajo en lápiz y papel.

Problema 1

• Usando el programa Regla y compás, construyan un cuadrilátero convexo.
• Señalen los puntos medios de sus lados.
• Investiguen qué tipo de cuadrilátero queda determinado con dichos puntos medios como vértices.
• ¿Sucederá lo mismo con otros cuadriláteros? Investiguen usando nuevamente el programa Regla y compás.

Se recomienda permitir que los alumnos indaguen individualmente para elaborar alguna conjetura.

Para obtener un cuadrilátero convexo en la pantalla del monitor usando el programa Regla y compás, los alumnos pueden optar por:1. Trazar cuatro rectas que al cruzarse "encierren" un cuadrilátero.

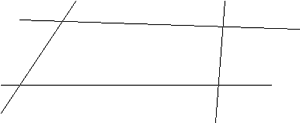2. Señalar cuatro puntos y unirlos por medio de segmentos consecutivos hasta cerrar la poligonal.

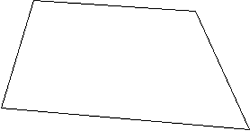
Una vez determinado el cuadrilátero, pueden hacer uso de la opción Punto medio que suministra el programa. Al unir dichos puntos medios aparecerá un paralelogramo. Inicialmente podrán advertir o no que se trata de tal tipo de figura. Usando la opción Mover podrán mover un vértice del cuadrilátero inicial y se hará más notorio que la figura interior es efectivamente un paralelogramo. Algunos alumnos manifestarán esto sin otro argumento que lo que "ven". Otros, en un intento de asegurarse, intentarán corroborarlo por medio de la opción Trazar rectas paralelas (al trazar la recta paralela a uno de los lados de la figura interior que pasa por un vértice opuesto "verán" que coincide con el lado opuesto).

Aquí es importante una primera puesta en común para que los alumnos argumenten acerca de sus conjeturas y de los procedimientos que han seguido para llegar a las mismas. A continuación es interesante plantear el problema 2.

Problema 2

"El cuadrilátero que tiene como vértices los puntos medios de los lados de otro cuadrilátero convexo es paralelogramo", ¿es una afirmación válida en cualquier caso?

En este momento se da el crucial paso entre lo que el alumno puede "ver" (sometido al riesgo de lo casual) y lo que puede asegurar sin necesidad de una representación concreta. Demostrar esta propiedad es darle rango de validez general a aquello que los "sentidos" nos manifiestan, es transitar con los alumnos del nivel de deducción informal al nivel de deducción formal que plantean los trabajos de Dina y Pierre Van Hiele.

En el caso de este problema, la deducción se puede hacer teniendo en cuenta la propiedad que dice que las bases medias de un triángulo son paralelas a los lados. Es importante, entonces, que se haya trabajado previamente en el descubrimiento de la propiedad de las bases medias del triángulo, para que los alumnos puedan echar mano de ella.

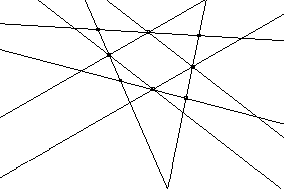
Se sugiere que, si no se les ocurre a los alumnos trazar, como elemento auxiliar de la demostración, la diagonal del cuadrilátero exterior (muy común para los que están transitando del nivel de deducción informal al nivel de deducción formal), el docente intervenga indicando este trazado, y a partir de allí los deje explorar.

Otras recomendaciones

• Como secuencia de trabajo se sugiere presentar estos mismos problemas para la exploración del cuadrado, rectángulo, rombo, paralelogramo, trapecio, para finalmente generalizar.
• Puede usarse la opción Especial y luego Texto del ejercicio, del programa Regla y compás, para presentar los enunciados de los problemas a los alumnos.

Contenidos

• Elaboración de conjeturas y pruebas.
• Generalización de soluciones.

Objetivos

• Elaborar conjeturas acerca de qué clase de cuadriláteros pueden obtenerse tomando como vértices los puntos medios de un cuadrilátero dado, y probarlas.
  

Autoras: Mabel Pujadas y Liliana Eguiluz

Para trabajar dependencia funcional y áreas

Principales nociones ligadas al concepto de función

Uno de los conceptos constitutivos de la noción de función, entendida como herramienta apta para modelizar fenómenos de cambio, es el de dependencia. La noción de dependencia implica la existencia de un vínculo entre cantidades y conlleva la idea de que un cambio en una de las cantidades tendrá efecto sobre las otras.

Pero la noción de dependencia es difícilmente identificable sin otra noción que puede considerarse como el verdadero punto de partida del concepto de función: la variabilidad. En efecto, el único medio de percibir que una cosa depende de otra es hacer variar cada una por vez y constatar el efecto de la variación.

Los principales elementos que integran la noción de función son, entonces -además de la correspondencia, la simbolización y las distintas formas de representación-, la variación y la dependencia.

La noción de función en la Educación Polimodal

En los contenidos básicos para la Educación Polimodal, la noción de función, sus diferentes formas de representación y el estudio detallado del comportamiento de las funciones más utilizadas adquieren mayor relevancia que en los ciclos anteriores. Del análisis de los CBC para Polimodal surge que se pretende que los alumnos continúen el estudio de las funciones, correspondiendo a este nivel un tratamiento más sistemático y profundo de las nociones de variable, parámetro y dependencia; las variables discretas y continuas; las distintas formas de representación de funciones (coloquial, gráfica, analítica, por tablas, etc.); la caracterización de los dominios o conjuntos de definiciones; y el uso de este concepto y sus limitaciones en la modelización de situaciones provenientes de la matemática y de otras áreas del conocimiento.

Todos estos elementos constitutivos del concepto que se mencionan en el párrafo anterior, así como algunas caracterizaciones, deberían aparecer en esta etapa de la escolaridad como recursos que permiten acceder a una mejor conceptualización de la noción de función, la que deberá jugar el papel de instrumento para resolver problemas.

En ocasiones, el deslizamiento del objeto de estudio hacia la algoritmización oculta el sentido de dependencia, de variación y de cambio, que se tornan significativos en la resolución de problemas. A causa de este deslizamiento, las definiciones que desarrollan muchos alumnos describen los usos que han hecho de las funciones y muestran que conciben la función como un cierto procedimiento, y en muy pocos casos la consideran como transformación de magnitudes variables.

En este sentido Ruiz Higueras (1998) concluye: "tanto se ha descompuesto el objeto función en segmentos para su enseñanza que el alumno no logra unificarlos dándoles una significación global. El alumno ha visto muchos objetos allí donde sólo debía existir uno".

Actividad para la enseñanza de algunos aspectos de la noción de función

Con este problema es posible introducir la idea de variación de una función definida sobre un intervalo, ya que se trata de analizar la variación del área de los rectángulos de igual diagonal, cuya base puede medir entre 0 y 6 unidades.

El programa Regla y compás permite a los alumnos interactuar con la figura construida variando las posiciones del punto M. Así podrán visualizar el modo en que las posiciones de los puntos D y E dependen de la posición del punto M.

Dado que el programa puede reconocer automáticamente las longitudes de los segmentos y calcular a partir de ellas el área buscada, los alumnos podrán concentrarse en el análisis de las variaciones sin realizar cálculos ni mediciones.

Se pretende favorecer la comprensión del problema mediante la manipulación de la figura, de manera que ciertas propiedades aparezcan como herramientas necesarias para resolver el problema y justificar la solución encontrada.

Para comenzar con el trabajo propuesto se puede utilizar la construcción ya realizada o volver a hacerla.

• Para utilizar la construcción ya realizada, hay que abrir el programa Regla y compás y luego el archivo "rectangulo.car".
• Para volver a hacer la construcción puede seguir las instrucciones.

Una vez que dispongan de la construcción, los alumnos podrán mover el punto M y explorar cómo varían las posiciones de los elementos que dependen de dicha posición y los valores de los parámetros asociados.

Se les puede pedir que busquen un intervalo del valor x (medida del lado AM) para el que el área f(x) sea máxima, y que identifiquen dicho rectángulo para un valor de x dentro de ese intervalo.

Durante este proceso formularán sus conjeturas y buscarán argumentos para defenderlas.

Al comenzar a buscar el área máxima es posible que los alumnos identifiquen como tal a la máxima que encuentren moviendo el punto M, o intenten hacerlo por ensayo y error a partir de las medidas de los lados sin apropiarse verdaderamente del problema dentro del marco geométrico.

Dado que la solución exacta es irracional y, por lo tanto, no podrán hallarla con el programa (los programas trabajan con una cantidad finita de decimales), los alumnos deberán buscar necesariamente una respuesta y su justificación por un método geométrico. Es decir, tendrán que identificar que, entre todos los rectángulos con diagonal fija, el cuadrado es el rectángulo de área máxima, y justificar la respuesta valiéndose de propiedades.

Una vez resuelto este problema y discutidas sus conclusiones es necesario plantear nuevas situaciones en las que los alumnos deban volver a emplear los elementos que han surgido.

Es posible profundizar la idea de variación de la función área de una familia de rectángulos inscriptos en un triángulo rectángulo, la que también estará definida sobre un intervalo. En este caso, el conjunto de los rectángulos definidos no tendrá un elemento fijo.

Una vez planteado el enunciado, el trabajo de los alumnos consistirá en construir las figuras con el programa y formular una serie de conjeturas. Conviene otorgar tiempo suficiente para que los alumnos puedan formular de forma efectiva sus conjeturas y determinar qué medidas es necesario que muestre el programa para estudiar la variación del área.

Si el triángulo rectángulo elegido es isósceles, nuevamente el rectángulo de área máxima será el cuadrado, pero, en general, para cualquier triángulo rectángulo, el rectángulo inscripto de mayor área será aquel que tenga un vértice en el punto medio de la hipotenusa.

Para probarlo, los alumnos podrán utilizar elementos de geometría analítica o comparar las áreas de los rectángulos que muestra el siguiente dibujo.

Comentarios

En la elección del problema inicial se tuvo en cuenta que está formulado dentro de un marco que resulta familiar a los alumnos: el marco geométrico, en el que se utilizan conocimientos que poseen los alumnos del nivel Polimodal.

Por otro lado, la situación puede hacer surgir la necesidad de:
- Estudiar la función que asocia AM con el área del rectángulo.
- Buscar una formulación algebraica para representar la función.

Esto permite poner en juego la articulación entre varios marcos.¹

Luego del trabajo realizado en el marco geométrico, es interesante resolver el mismo problema en el marco algebraico.

En este marco, se puede estudiar la correspondencia que existe entre los puntos del gráfico de la función Área del rectángulo y los rectángulos analizados.

Por ejemplo, en el gráfico de f(x)= , la abscisa del máximo corresponde al lado del cuadrado.

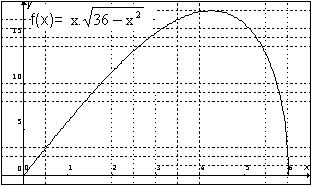
En este caso, el gráfico es uno de los elementos esenciales para acceder a diferentes significaciones de la noción de función y no es en sí mismo un punto de llegada.

Finalmente, cabe mencionar que el programa Regla y compás proporciona una herramienta válida para explorar las variaciones del área al variar la figura, pero, a su vez, presenta limitaciones que es necesario tener en cuenta. Es decir, puede servir para una primera validación de las conjeturas de los alumnos, pero es necesario avanzar hacia la producción de prueba de las mismas.

Por ejemplo, al buscar el rectángulo de área máxima se puede obtener la siguiente figura:

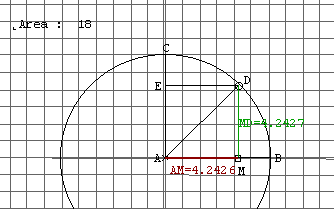
En la figura se leen distintas longitudes en los lados, aun cuando ya se sospecha que la solución es el cuadrado. Es momento entonces de discutir con los alumnos el tema de "las aproximaciones" que proporciona el software, ya que tiene límites en las aproximaciones decimales y surgirá la necesidad de buscar argumentos que permitan transformar la sospecha o conjetura en una afirmación.

Bibliografía consultada

Alayo, F., "Funciones y gráficas", en Suma, España, 1989, vol. 4.
Azcárate, C. y J. Deulofeu Piquet, Funciones y gráficas, Síntesis, 1996.
Barallobres, G., "Funciones", Documento Curricular, Municipalidad de la Ciudad de Buenos Aires, 1998.
Chemello, G. y Díaz, "Matemática. Modelos didácticos", Prociencia, Buenos Aires, Conicet, 1996.
"Documentos de actualización curricular en Matemática", n° 1 y 4, Municipalidad de la Ciudad de Buenos Aires, 1996-1997.
Douady, R., Juegos de marcos y dialéctica instrumento-objeto en la enseñanza de la matemática, Universidad de París, 1984.
Grupo "Lycée" del IREM de Clermont-Ferrand. "Introducción a la noción de función en seconde", en La enseñanza de las matemáticas: puntos de referencia entre los saberes, los programas y las prácticas, Francia, Topiques Editions, 1996.
Hanfling, M. y otros, "Matemática. Temas de su didáctica", Prociencia, Buenos Aires, Conicet, 1997.
Hitt Espinosa, F., "Sistemas semióticos de representación del concepto de función y su relación con problemas epistemológicos y didácticos", en Investigaciones en Matemática Educativa, México, Grupo Editorial Iberoamérica, 1996.
Piquet, J. D., "Concepciones de los alumnos de Secundaria sobre distintas gráficas de funciones", en Uno, Revista de Didáctica de las Matemáticas, GRAO Educación, España, 1995, N° 4.
Ruiz Higueras, L., La noción de función: análisis epistemológico y didáctico, España, Universidad de Jaén, 1998.
---, Una aproximación a las concepciones de los alumnos de secundaria sobre la noción de función. Memoria de Tercer Ciclo, Universidad de Granada, 1991.

^1. R. Douady define: "Un marco está constituido por objetos de un mismo dominio y por las relaciones entre estos objetos. Podemos hablar de marcos geométrico, numérico, algebraico, etc."

Autora: Mirta Irene Grines de Hanfling